This project aims to devise a methodology to accurately model color-pigment mixing onto a multi-dimensional color space to holistically map mathematical quantification of the chemistry behind hair color to the full human perception color gamut. The system formulates precise color predictions and visualizations by designing a multi-output machine learning model (Python), with regression analysis, and MATLAB multi-dimensional vector color plots.

The dataset underpinning this endeavor is a comprehensive repository of 29,000 formulations, each uniquely defined by specific ratios of seven primary hair color ingredients: Black, Brown, Blonde, Clear, Red, Blue, and Yellow. To elevate predictive accuracy, the project employs an advanced MultiOutputRegressor, utilizing a linear regression base estimator to forecast HEX codes for each unique formulation. The model uses Kubelka-Munk equations for training, which aim to provide a more accurate physical representation of the pigment in the real world, beyond the confines of a purely digital RGB mix. This becomes especially significant in the context of hair color variation when subjected to physical application with additional chemicals such as oxidants and ammonia.

In the analytical phase, the project strategically employs visualizations based on CMYK, HSL, and CIE-lab color spaces. This choice is driven by the subtractive nature of hair color, and the nuanced level system inherent in hair color shades ranging from dark (level 1) to light (level 10). The visualizations not only guide the formulation optimization process but also serve as a crucial component in the project’s innovative approach. Plotting it on CIE-Lab helps retain the importance of color perception while formulating the machine learning framework. The results obtained from this integrated approach showcase the effectiveness of the proposed methodology in accurately predicting diverse hair color shades. The project’s significance extends beyond the realms of predictive accuracy, as evidenced by its potential for real-world applications within the beauty industry. The strategic use of CIE-lab visualizations, coupled with the two-phased method incorporating Kubelka-Munk theory, positions this project at the forefront of hair color technology.

(Note: This project was formulated parallel to my role as a Color Algorithm Data Analyst at YUV. Consequently, certain specifications for exact formulations, dispensing techniques, and swatching logic are not shared for privacy reasons).

Link to the GitHub Repository for all code files can be found here.

1. Data Preparation and Machine Learning Model Training:

The first step is training a machine learning model to accurately predict a HEX code for any input color formula that has mixing ratios for: Black, Brown, Blonde, Clear, Red, Blue, Yellow, pH Booster, Dev strength, and Dev ratio as input pigments. The dataset comprises 29,000 formulations with specific ingredient ratios. My approach involves a MultiOutputRegressor model, addressing the interdependence of Red (R), Green (G), and Blue (B) channels in HEX codes.

1.1 Training Dataset:

The input data is in the form of a CSV file with 11 columns 30000 color formulae and associated HEX codes.

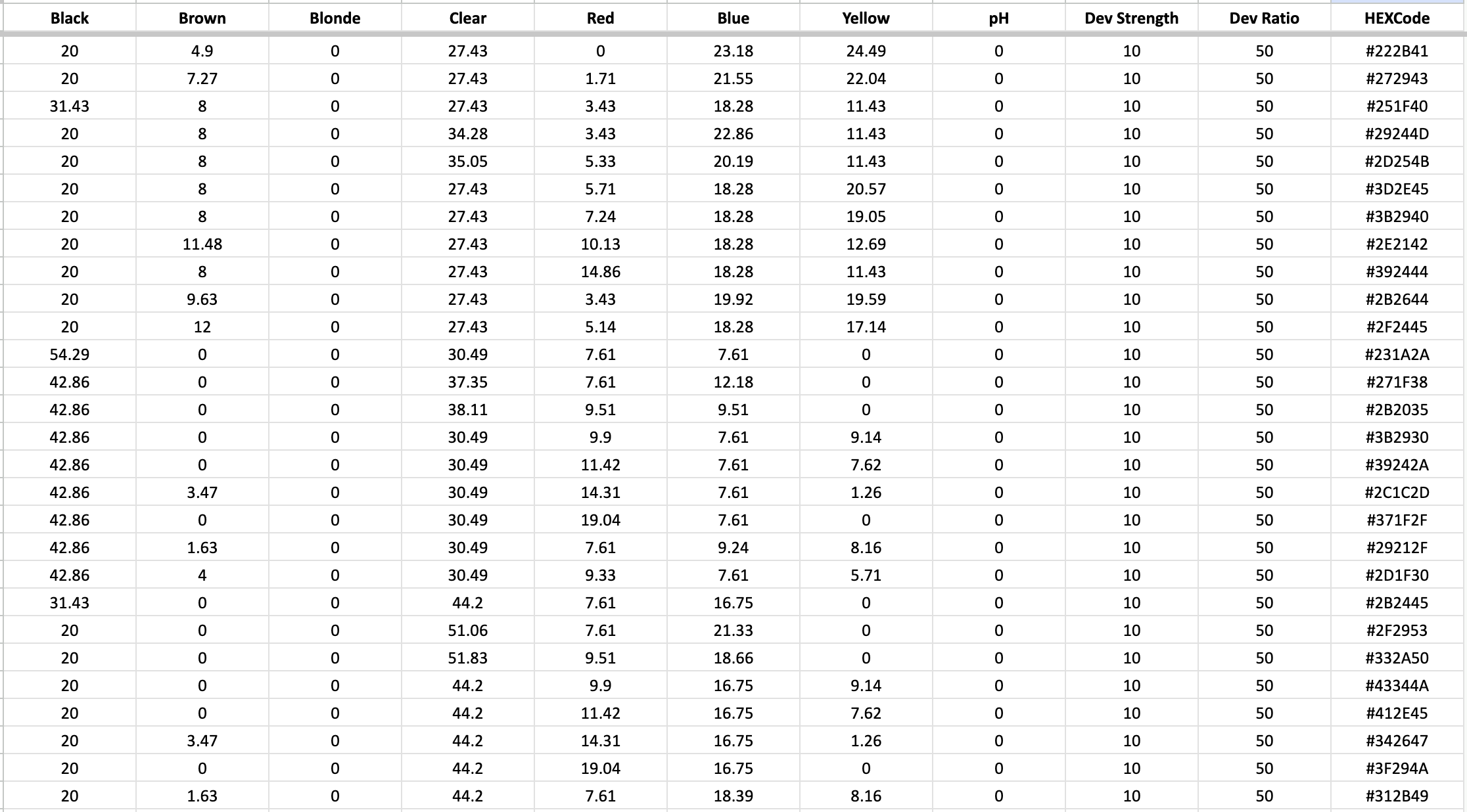
Note: The input dataset for the model is true color formulations generated using algorithms I designed for YUV, each associated with a specific hair color shade. The shade names have not been revealed for privacy reasons.

What is a HEX Code?:

To measure HEX codes for the existing dataset, the formula was swatched using the YUV device and a spherical spectrophotometer gave the right RGB value, which was concatenated and converted to a HEX code to reduce training time for the multi-output regression model.

1.2 Train a Multi-Output Regression Model:

The input dataset is randomly split into a training set and a validation set. The complete code for the Multi-output Regression Model can be found here.

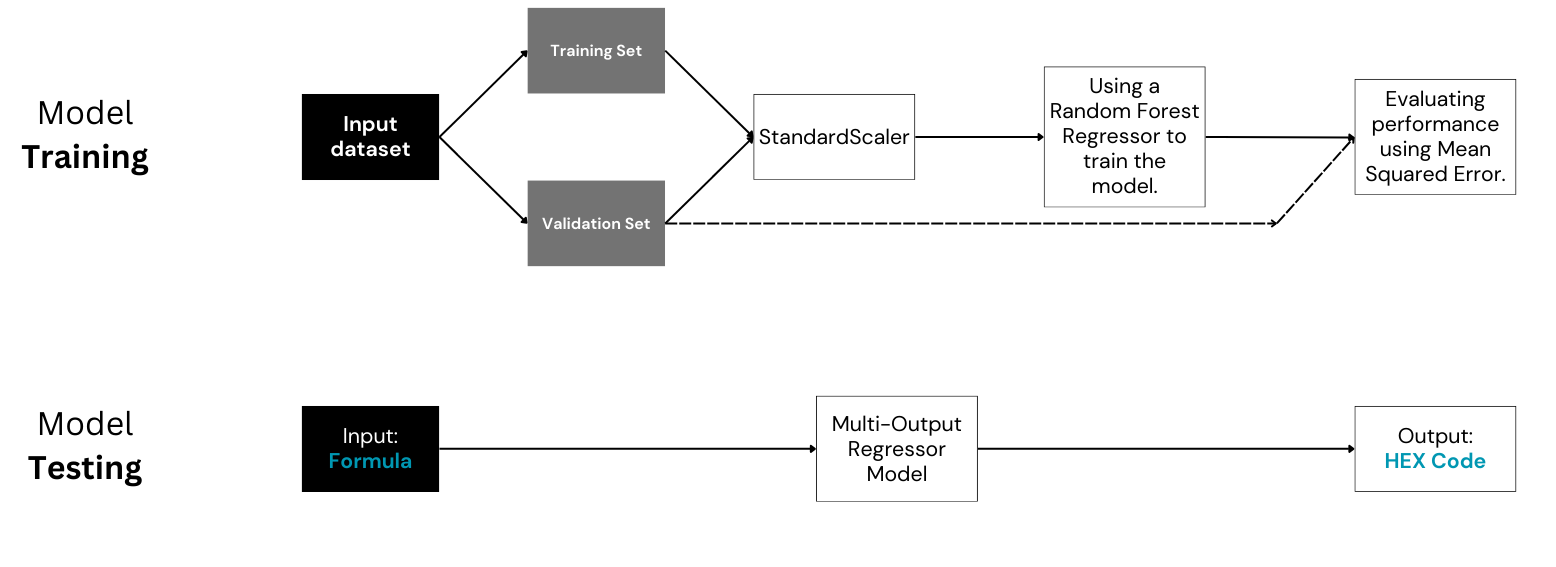
The provided Python code employs a MultiOutputRegressor model, utilizing a Random Forest Regressor as the base estimator, to predict HEX codes for hair color formulations based on ingredient ratios. The input comprises a CSV dataset with columns representing the ratios of Black, Brown, Blonde, Clear, Red, Blue, Yellow, pH, Developer Strength, and Developer Ratio. The target is the corresponding HEX code for each formulation. The code first loads the dataset and splits it into training and validation sets. It then standardizes the data using StandardScaler and initializes the MultiOutputRegressor model. After training the model on the training set, it predicts HEX codes for the validation set and evaluates the performance using Mean Squared Error. To use the trained model for predictions on new formulations, prepare the input data for the new formulation, standardize if necessary, and use the predict method of the trained model. The Mean Squared Error on the validation set serves as a metric for model performance during training.

1.3 Kubelka-Munk Theory Integration:

Theory: The Kubelka-Munk theory is a mathematical model used to describe the optical properties of pigmented materials, particularly in the context of color mixing and reflection. It accounts for interactions between light and pigment layers within a material.

Equations: The theory is commonly expressed through the Kubelka-Munk equations, which describe how light interacts with a stack of pigment layers. For a single layer, the equations are as follows:

Values for R0 and K were calculated using the spherical spectrophotometer and t is defaulted at 2mm for each of the 10 input pigments. In the context of predicting hair color, integrating the Kubelka-Munk theory into the training loop offers a more realistic representation of pigment behavior. Here’s how it’s implemented in the Multi-output Regression model.

1. Simulation of Color:
   • Using the Kubelka-Munk equations, the model simulates the color of a hair formulation based on the known properties of pigments and their interactions within hair.
2. Custom Loss Function:
   • The model defines a custom loss function that incorporates the simulated color alongside the predicted and actual colors.
   • This loss function guides the optimization process, ensuring the model considers both predicted RGB values and the color representation obtained through the Kubelka-Munk simulation.
3. Training Loop:
   • The Kubelka-Munk simulation is integrated within the training loop, making it a part of the forward pass and it optimizes the model parameters considering the combined loss from both predicted and simulated colors.
4. Optimization Outcome:
   • The model learns to adjust its parameters not only based on observed RGB values but also by considering how pigments interact and influence the resulting color in a realistic setting by integrating the Kubelka-Munk equations.

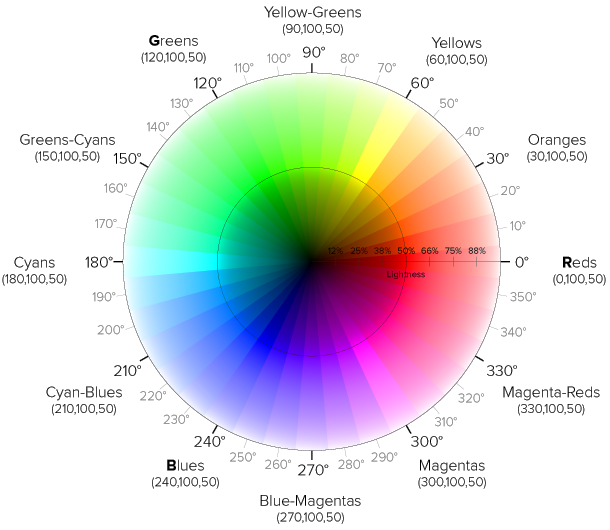
2. Mathematically Extract CMYK, HSL, and CIELa*b* Coordinates:

The output of the part 1 model is a system designed to convert any input color pigment formula to an output HEX code. This enables me to convert all 9 million color formulations that I generate at work, to HEX codes consequently allowing me to map them to a vector color space. Hair color works on a level system, with L1 being the darkest and L10 being the lightest. As pigment mixing for hair color results in a black end result, using a subtractive vector color space to map the HEX values is a logical choice. The HEX itself is derived from an RGB color space, which is additive as the end result is white. Therefore, the first step is to convert the hex code from part 1 to the following subtractive color spaces:

CMYK	HSL	CIE-La*b*
Subtractive	Subtractive	Subtractive
Used in color printing, representing colors as a combination of cyan, magenta, yellow, and black, where “K” stands for the key (black) channel.	Representing colors based on their Hue (type of color), Saturation (intensity or vividness), and Lightness (brightness).	Provides a perceptually uniform representation of colors, with dimensions L* for lightness, a* for the color on the green to red axis, and b* for the color on the blue to yellow axis.

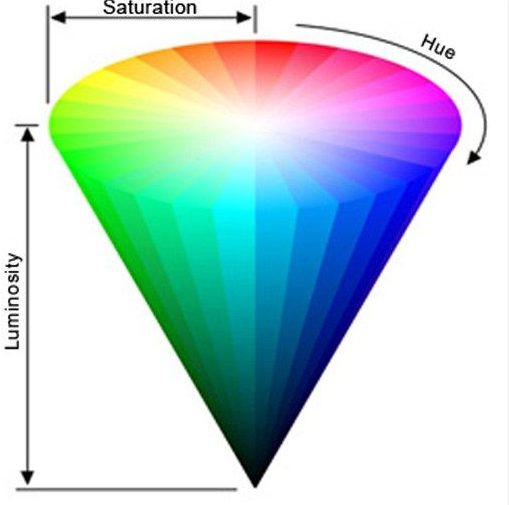
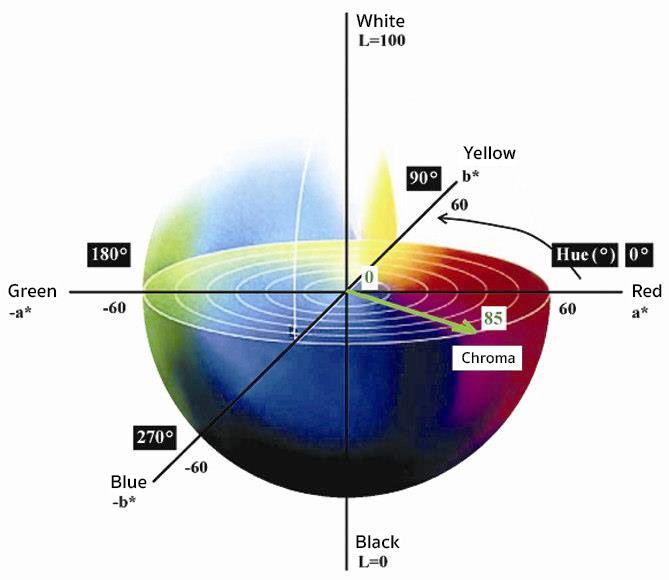
3. Plotting Coordinates in Three Parallel Vector Color Spaces:

The existing HEX codes are then converted to CMYK, HSL, and CIELa*b* using the Python script here and visualized using Matplotlib:

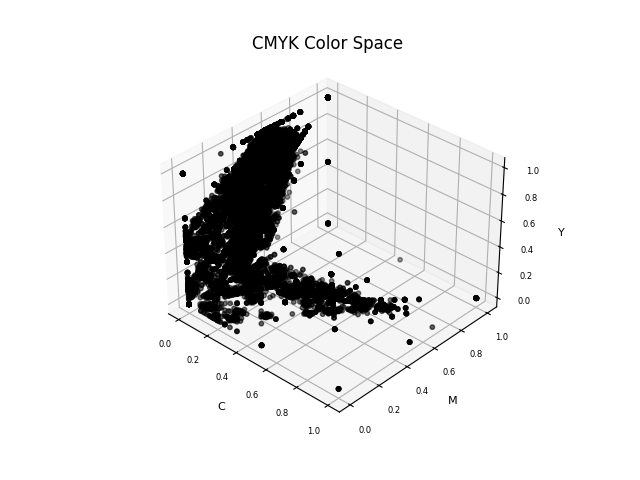
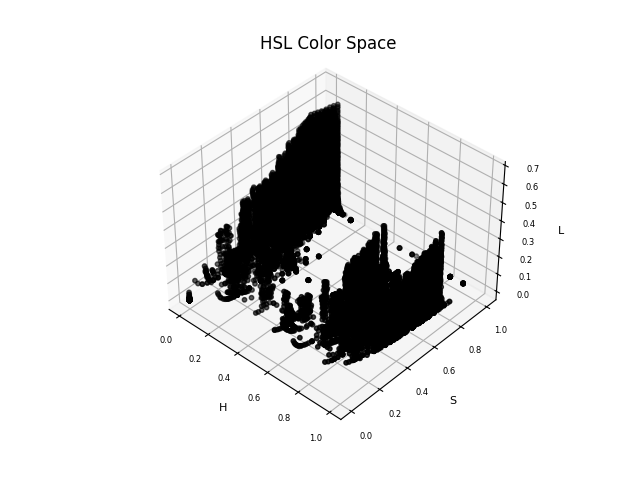
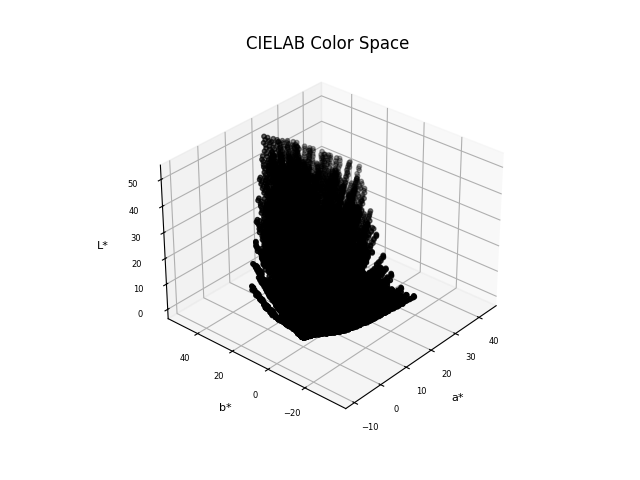
By plotting the same color across three-dimensional spaces for 3 different color dimensions, it’s easier to map out how the entire color palette sits across a hue-saturation spectrum and a visual perception spectrum. However, the high variance is visually identifiable in the CMYK and HSL color plots. Hair color is heavily affected by chemical factors, which alter the end visual result dramatically.

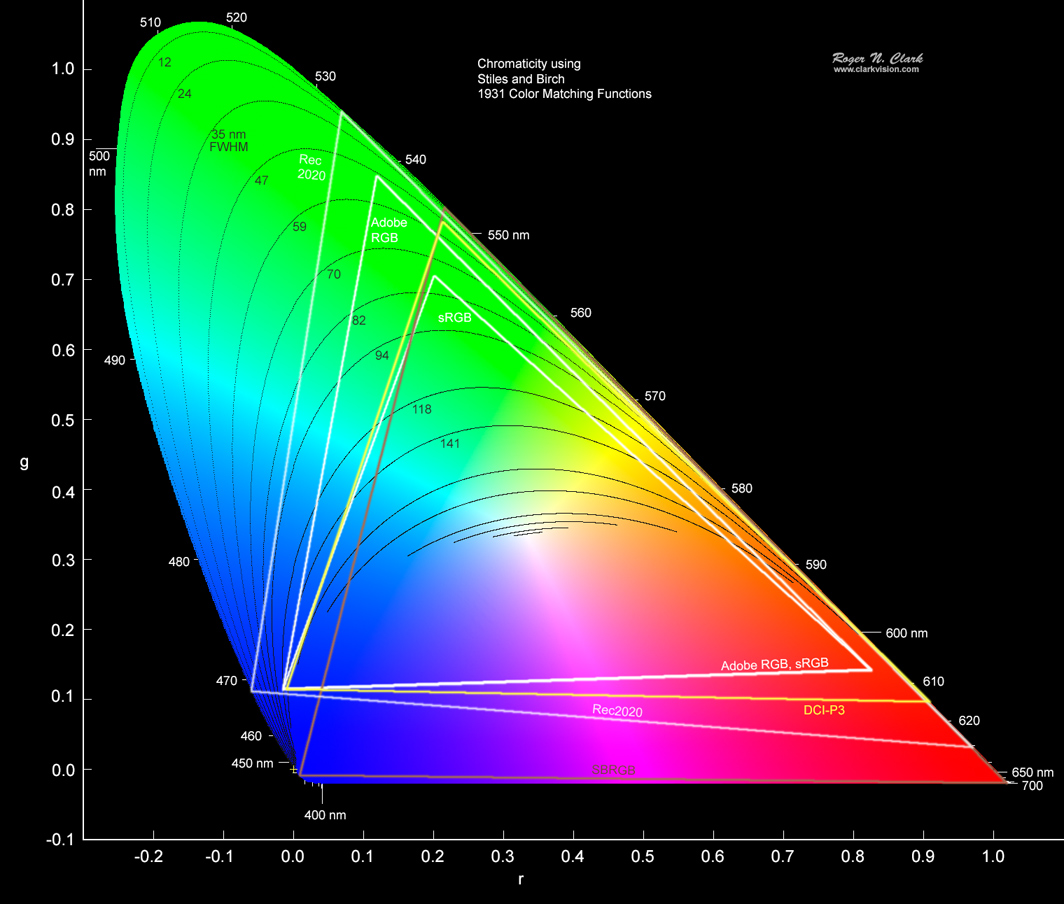
Therefore, using a color space like CMYK is quite restrictive because when you compare the overall chromaticity diagram (Image 3), CMYK and RGB are both quite restrictive in the visual color spectrum they allow. CIELAB, however, recreates the complete gamut of human vision and therefore provides the right dimensionality to map hair color formulae to.

4. Averaging Plots to a Single CIELAB Visualization:

The machine learning model from step 1 attempts to algorithmically quantify chemical changes from pigment to color. Now, I use existing HEX values and generated HEX values for 100000 color formulae to map the color algorithm onto a CIELa*b* vector space:

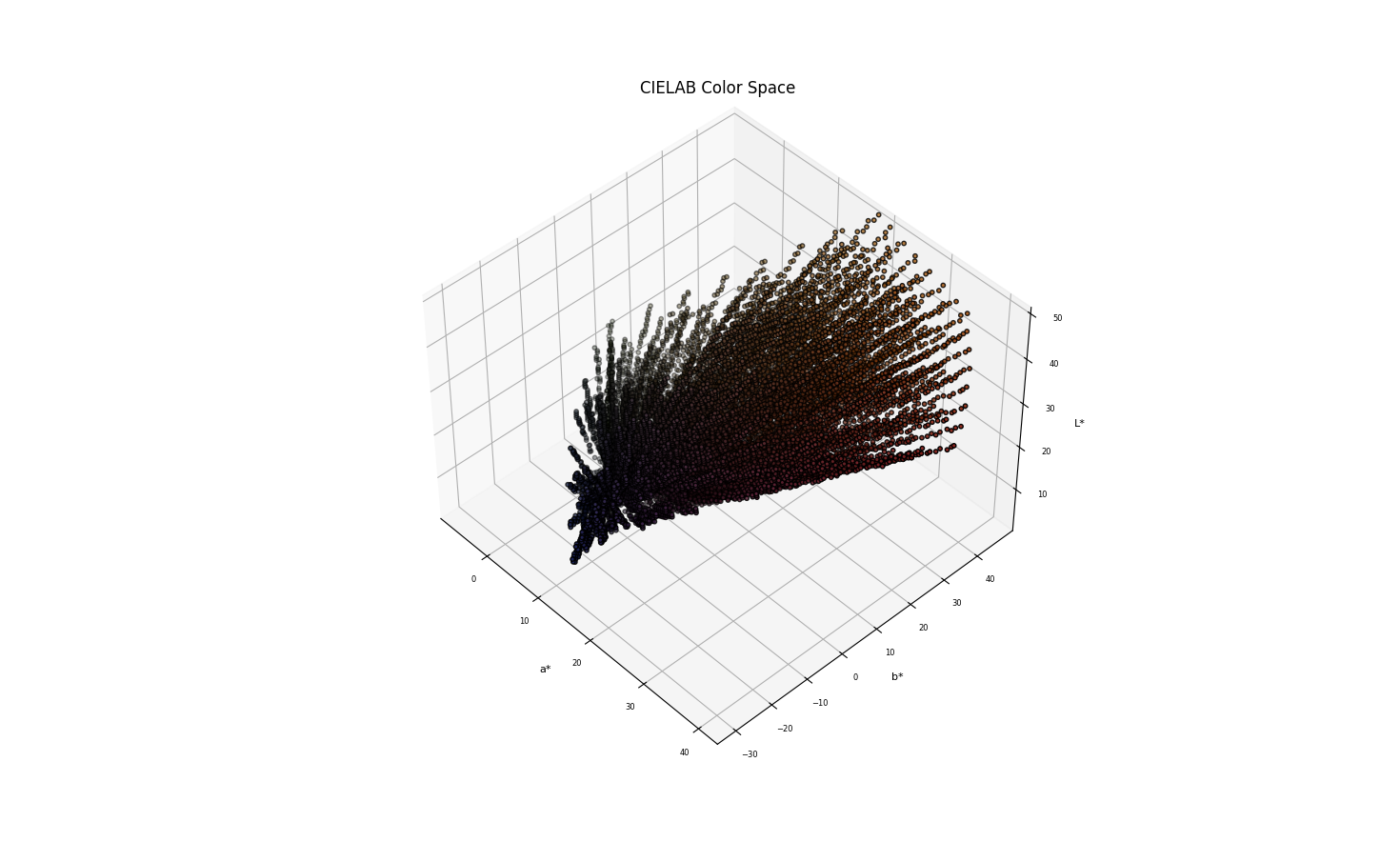
To create this plot, the code was modified to make the color coordinates more accurate by averaging the plots of RGB, HSL, and CMYK coordinates into a single CIELAB visualization. A machine learning model functions best on self-improvement as it’s fed more data. Therefore, I am in the process of batch training it on all 9 million formulations generated by color quantification algorithms I design at work. I am experimenting with different hyperparameters (learning rates, number of layers, nodes per layer) to optimize the MultiOutput Regression model. I also periodically retrain the model with the updated dataset to adapt to new formulations and improve accuracy.

5. Conclusion:

Color is very mathematical in nature, digital color and physical color have a higher mathematical dimensionality because there are physical factors such as reflectance and chemical mixing that function differently on screen and when dealing with actual pigments. Quantifying the chemistry behind color science and applying it to hair color is my role at work, which helped me generate 9 million possible formulations with varying ratios of 10 base ingredients: ’Black’, ‘Brown’, ‘Blonde’, ‘Clear’, ‘Red’, ‘Blue’, ‘Yellow’, ‘pH’, ‘Developer Strength’, and ‘Developer Ratio’. However, to truly realize the potential of the algorithm, I need to be able to visualize the shades together, which is tricky because digital color mixing only functions with RGB color spaces that don’t capture the visual dimensionality gamut for human perception (Image 4). This project successfully manages to quantify, modify and visualize the formulations on a digital color space, which allows for the training of further machine learning models to help predict any possible hair color formulation in the future, working backwards from a target shade number and associated visual color reference.

---

Additional Links:

GitHub Repository for all scripts for this project: Link